

1. 배치 경사 하강법.
지금까지 사용한 경사하강법 알고리즘은 알고리즘을 1번 반복할때 1개의 샘플을 사용하는 확률적 경사 하강법을 사용 했습니다.
이 방법은 가중치를 1번 업데이트 할때마다 1개의 샘플을 사용하므로 손실함수의 전역 최솟값을 불안정하게 찾습니다.
배치 경사 하강법은 가중치를 1번 업데이트 할대 전체의 샘플을 사용하므로 손실 함수의 전역 최솟값을 안정적으로 찾을 수 있습니다.
하지만 배치 경사 하강법은 전체샘플을 계산하므로 계산량이 매우 많습니다.
즉, 우리는 배치 경사 하강법을 효율적으로 사용하기 위해 연산에 대해 알아 볼 필요가 있습니다.!
2.벡터화된 연산 & 행렬 연산.
이때까지 정방향 계산을 할때 가중치와 입력을 각각 곱하여 더했습니다.
z = np.sum(self.w * x) + self.b
위식을 self.w * x와 같이 나타낼 수 있었던 이유는 넘파이의 원소별 곱셈 기능 덕분이였습니다 .
두벡터를 곱하는 스칼라곱을 행렬계산으로 어떻게 바꿀 수 있을까요?
x = [x1,x2 ... xn]
w = [w1,w2 ... wn] 으로 표현해 보면 ,

위와 같이 바꿀 수 있습니다.
이제 좀더 나아가 전체 샘플에 대한 가중치 곱의 합을 행렬곱셈으로 구해봅시다.
만약 훈련데이터가 m개의 샘플 , 3개의 특성을 가지고 있다고 합시다. X,W를 활용하면 ,
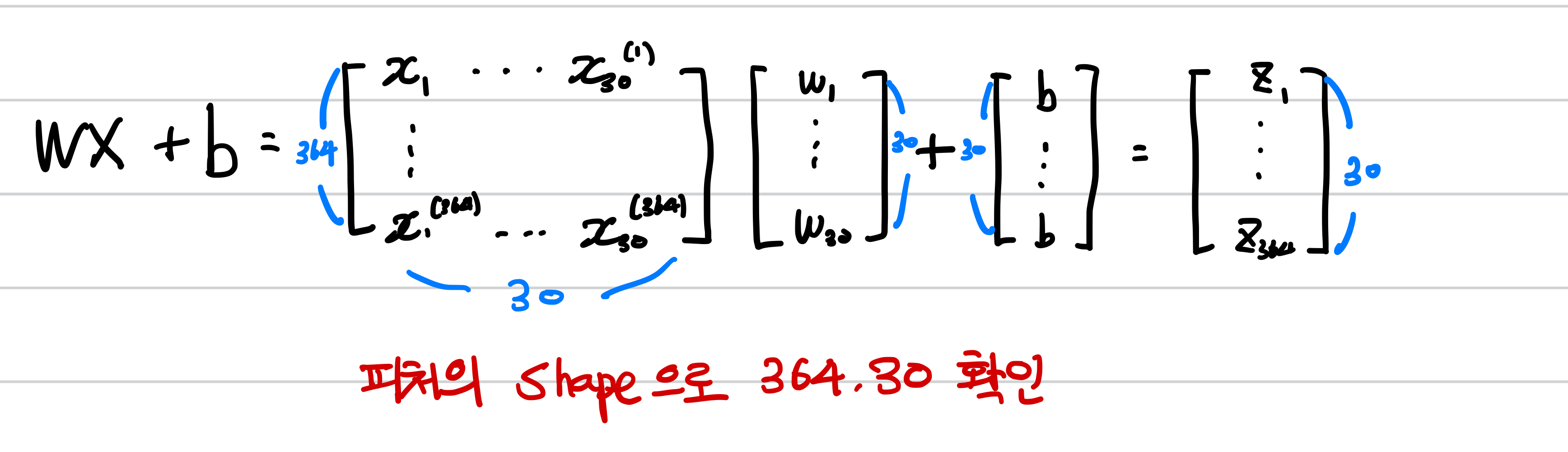
이제 이러한 행렬계산을 바탕으로 SingleLayer클래스에 적용해봅시다.
3. SingleLayer 클래스에 배치 경사 하강법 적용하기
3-1) 정방향 계산을 행렬곱셈으로 표현하기.

3-2) 그레디언트 계산.
X.T는 계산을 위해 X를 전치한 것이고 E는 오차를 나타낸 행렬입니다.

4.forpass() , backprop() 메서드에 배치 경사 하강법 적용.
def forpass(self, x):
z = np.dot(x, self.w) + self.b # 선형 출력을 계산합니다.
return z
def backprop(self, x, err):
m = len(x)
w_grad = np.dot(x.T, err) / m # 가중치에 대한 그래디언트를 계산합니다.
b_grad = np.sum(err) / m # 절편에 대한 그래디언트를 계산합니다.
return w_grad, b_grad
5. fit() 메서드 수정하기.
확률적 경사 하강법에서는 샘플을 순회하기 위한 for문이 있었지만 배치 경사 하강법은 한꺼번에 계산 했으므로 for문을 삭제합니다.
def fit(self, x, y, epochs=100, x_val=None, y_val=None):
y = y.reshape(-1, 1) # 타깃을 열 벡터로 바꿉니다.
y_val = y_val.reshape(-1, 1)
m = len(x) # 샘플 개수를 저장합니다.
self.w = np.ones((x.shape[1], 1)) # 가중치를 초기화합니다.
self.b = 0 # 절편을 초기화합니다.
self.w_history.append(self.w.copy()) # 가중치를 기록합니다.
# epochs만큼 반복합니다.
for i in range(epochs):
z = self.forpass(x) # 정방향 계산을 수행합니다.
a = self.activation(z) # 활성화 함수를 적용합니다.
err = -(y - a) # 오차를 계산합니다.
# 오차를 역전파하여 그래디언트를 계산합니다.
w_grad, b_grad = self.backprop(x, err)
# 그래디언트에 페널티 항의 미분 값을 더합니다.
w_grad += (self.l1 * np.sign(self.w) + self.l2 * self.w) / m
# 가중치와 절편을 업데이트합니다.
self.w -= self.lr * w_grad
self.b -= self.lr * b_grad
# 가중치를 기록합니다.
self.w_history.append(self.w.copy())
# 안전한 로그 계산을 위해 클리핑합니다.
a = np.clip(a, 1e-10, 1-1e-10)
# 로그 손실과 규제 손실을 더하여 리스트에 추가합니다.
loss = np.sum(-(y*np.log(a) + (1-y)*np.log(1-a)))
self.losses.append((loss + self.reg_loss()) / m)
# 검증 세트에 대한 손실을 계산합니다.
self.update_val_loss(x_val, y_val)
지금까지는 하나의 층에 하나의 뉴런을 사용했습니다. 이제부터 층과 뉴런의 개수를 늘려 봅시다.
- 하나의 층에 여러 개의 뉴런.
다음은 3개의 특성과 2개의 뉴런이 있는 경우입니다.

3개에 특성에 해당되는 3개의 가중치와 각 뉴런마다 하나씩은 절편이 붙어 z를 도출 하였습니다.
또한 각 뉴런에 대해 도출된 z를 활성화 함수에 통과 시키고 각각의 가중치를 부여해 하나의 출력으로 나타내야 합니다.

- 은닉층의 등장 -
이제 앞에서 본 일련의 과정들을 하나의 그림으로 살펴 보겠습니다.

여기서 입력과 출력을 행려로 나타내게 되면,

와 같이 간단하게 표현 됩니다.
★ 정리
2개의 층을가진 신경망은 입력행렬 X, 첫번째 층의 가중치 행렬 W1과 절편 b1 첫번째 층의 출력 Z1 첫번째층의 활성화 출력 A1, 두번째 층의 가중치 행렬 W2 절편, 두번째 층의 출력 Z2로 나타낼 수 있다.

다층 신경망에 경사 하강법 적용하기.

- 출력층 -
1. 가중치에 대하여 손실함수를 미분합시다.(출력층)
W2에 대해 손실함수의 미분을 연쇄 법칙으로 풀어 계산해 보자.

먼저 앞에서 설펴본 손실 함수의 미분을 살펴보면
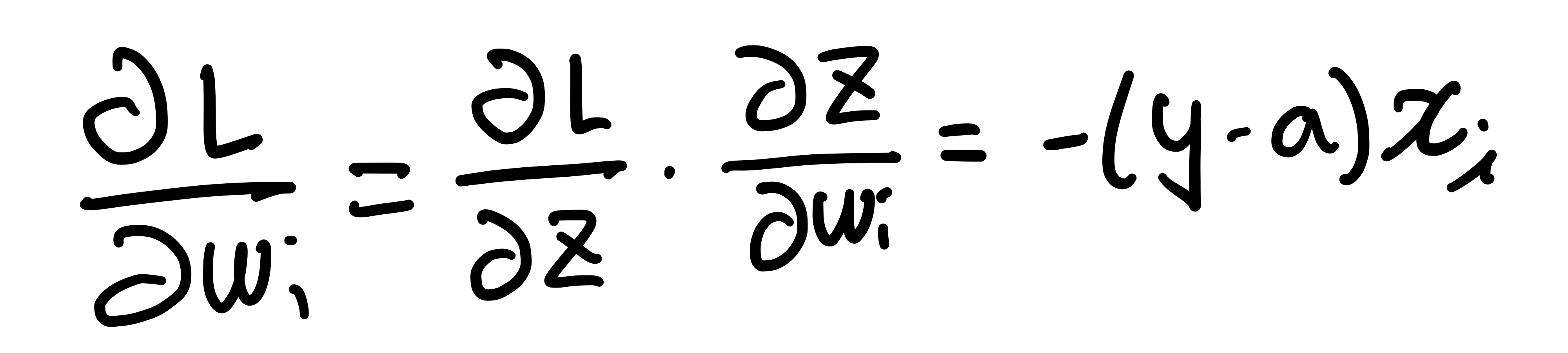
과 같이 결과값이 나온다는걸 이미 알고 있습니다.
여기서의 미분을 우리는 행렬로 확장만 시키면 됩니다.

2. 도함수를 곱합니다.(출력층)
이제 -(Y-A2)와 A1을 곱하기만 하면 됩니다. 하지만 행렬의 곱을 할때는 항상 크기에 주의해야 합니다. 각가의 행렬의 크기를 알아봅시다.
-(Y-A2)의 행렬 크기는 Y가 (m,1) , A2가 (m,1)이므로 크기는 (m,1) 입니다.
그렇다면 A1의 크기는 어떻게 될가요?
A1은 첫번째 가중치행렬 W1 과 입력 데이터 X를 입력 받고 이를 활성화 함수를 통과시킨 값입니다. 즉 , 데이터의 샘플의 크기와 뉴런의 갯수가 이 행렬의 크기가 되는 겁니다. (m,2)

그러면 이제 두 행렬을 곱해봅시다. 어떻게 곱하면 될까요 ? 바로 A1행렬을 전치하여 곱하면 됩니다.!

여기서 구한 가중치에 대한 그레디언트는 모든 샘플에 대한 그레디언트의 총합을 구한것입니다. 가중치 행렬을 업데이트하기 위해서 평균 그레디언트를 구해야 합니다. 그다음 적절한 학습율을 곱해 w2를 업데이트 합니다.
가중치에 대한 손실함수를 미분했으므로 이제 절편에 대한 손실함수 미분을 하겠습니다.
2. 절편에 대하여 손실함수를 미분합시다.(출력층)
다음은 신경망에 절편에 대한 손실 함수의 미분까지 표시한 것입니다.
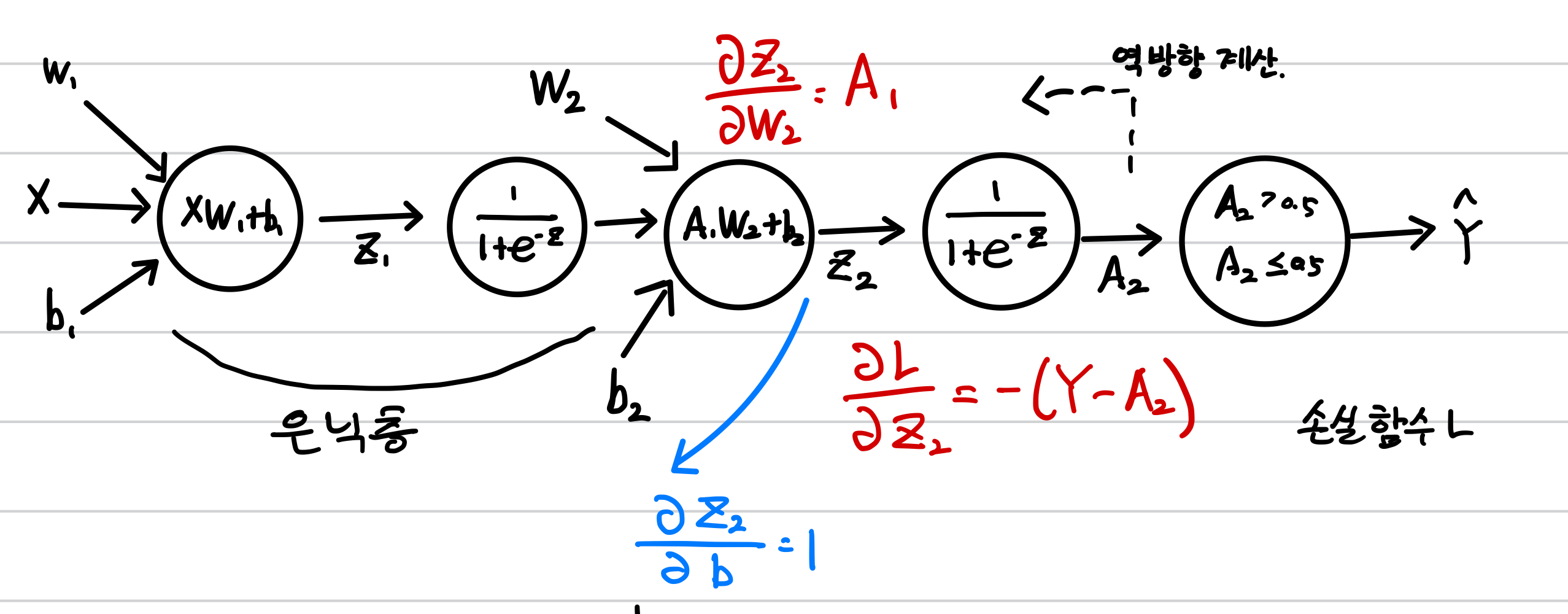
절편도 가중치에 대한 미분과 동일합니다.

이렇게 해서 출력층에서의 그레디언트를 모두 구했습니다.
-은닉층-
1.가중치에 대하여 손실 함수를 미분(은닉층)
가중치 W1에 대하여 손실 함수를 미분은 다음과 같은 연쇄법칙으로 나타낼 수 있습니다.

흐름도를 참고하면 한눈에 볼 수 있습니다.
-흐름도-

각각의 미분을 계산해 보면,

과 같습니다.
2. 도함수를 곱합니다.(은닉층)
곱하는 과정을 나누어 생각해 보면 ,
1) 두 도함수를 곱하는 의미는 각 샘플이 만든 오차를 출력층에 있는 2개의 뉴런에 반영시키는 것입니다.

2) 두행렬의 크기가 같으므로 원소별 곱셈을 할 수 있습니다.

3) 이제 오차의 그레디언트가 활성화 함수를 통과했습니다. 이 오차 그레디언트를 W1에 적용합시다.
Z1에 대한 W1의 미분이 X(m,3)이므로 전치하여 곱합니다.

이렇게 해서 가중치에 대하여 손실 함수를 미분하고 도함수를 곱해보았습니다.
마찬가지로 , 절편에 대하여 손실 함수를 미분하고 도함수를 곱해보면 다음과 같습니다.

2개의 층을 가진 신경망 구현하기
- SingleLayer 클래스와 다른점 -
1. SingleLayer 클래스를 상속받아 DualLayer 클래스 구현.
2. __init__() 메서드에 은닉층의 갯수를 지정하는 변수 추가.
(은닉층 , 출력층의 가중치 절편저장 , 은닉층의 활성화 출력 a1 저장.)
3.forpass() 메서드 수정.
> 은닉층의 활성화 함수를 통과한 a1과 출력층의 w2 곱하고 b2 더하여 최종 출력 z2 도출합니다.
4.backprop() 메서드 수정.

5. fit() 메서드 수정.
5-1 ) fit() 메서드에 있던 가중치 초기화 부분을 init_weight() 메서드로 분리했습니다. n_features는 입력 특겅의 개수를 지정하는 매개변수 입니다.
def init_weights(self,n_features):
self.w1 = np.ones((n_features , self.units)) #(특성 개수 , 은닉층 크기)
self.b1 = np.zeros(self.units) #은닉층 크기
self.w2 = np.ones((self.units , 1)) # (은닉층의 크기 ,1)
self.b2 = 05-2) fit() 메서드에 있던 for문 안에 있는 코드 중 일부를 training() 메서드로 분리 합니다.
def training(self , x, y ,m):
z = self.forpass(x)
a = self.activation(z)
err = -(y-a)
#오차를 역전파 하여 그레디언트 계산.
w1_grad , b1_grad , w2_grad , b2_grad = self.backprop(x,err)
#그레디언트에서 패널티 항의 미분값 뺀다.
w1_grad += (self.l1*np.sign(self.w1) + self.l2*self.w1) / m
w2_grad += (self.l1*np.sign(self.w2) + self.l2*self.w2) / m
# 은닉층의 가중치와 절편을 업데이트
self.w1 -= self.lr * w1_grad
self.b1 -= self.lr * b1_grad
self.w2 -= self.lr * w2_grad
self.b2 -= self.lr * b2_grad
return a5-3) 수정된 fit() 문
def fit(self,x,y,epochs=100,x_val=None,y_val=None):
y = y.reshape(-1,1) # 타겟을 열 벡터로 바꾼다.
y_val = y_val.reshape(-1,1)
m = len(x)
self.init_weights(x.shape[1]) #은닉층과 출력층 가중치 절편 초기화
#epochs 만큼 반복
for i in range(epochs):
a = self.training(x,y,m)
a = np.clip(a,1e-10 , 1-1e-10)
#로그 손실과 규제 손실을 더하여 리스트에 추가.
loss = np.sum(-(y*np.log(a) + (1-y)*np.log(1-a)))
self.losses.append((loss + self.reg_loss()) / m)
#검증 세트에 대한 손실 계산.
self.update_val_loss(x_val,y_val)6) reg_loss() 메서드 수정하기.
> 이 메서드는 은닉층과 출력층의 가중치에 대한 L1, L2 손실을 계산합니다.
def reg_loss(self):
#은닉층과 출력층의 가중치에 규제를 적용
return self.l1 *(np.sum(np.abs(self.w1) + np.sum(np.abs(self.w2))) + \
self.l2 /2*(np.sum(self.w1**2) + np.sum(self.w2**2)))이제 수정된 클래스를 바탕으로 훈련을 시켜보고 그에 따른 손실함수를 그래프를 살펴 보겠습니다.
dual_layer = DualLayer(l2=0.01)
dual_layer.fit(x_train_scaled, y_train,
x_val=x_val_scaled, y_val=y_val, epochs=20000)
dual_layer.score(x_val_scaled, y_val)
============================
0.978021978021978
import matplotlib.pyplot as plt
plt.ylim(0,0.3)
plt.plot(dual_layer.losses)
plt.plot(dual_layer.val_losses)
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train_loss','val_loss'])
plt.show()
손실함수가 감소하는 그래프가 이상적으로 매끄럽지가 않습니다. 이를 해결하는 방법은 무엇일까요??
이러한 현상이 생기는 이유는 가중치의 초기화와 관련이 깊습니다. 우리는 이때까지 가중치를 1로 고정 초기화를 시켜주었습니다. 이번에는 random.normal() 함수를 사용하여 정규 분포를 따르는 무작위 수로 가중치를 초기화 해봅시다.!
class RandomInitNetwork(DualLayer):
def init_weights(self, n_features):
self.w1 = np.random.normal(0, 1,
(n_features, self.units)) # (특성 개수, 은닉층의 크기)
self.b1 = np.zeros(self.units) # 은닉층의 크기
self.w2 = np.random.normal(0, 1,
(self.units, 1)) # (은닉층의 크기, 1)
self.b2 = 0동일한 방법으로 손실함수그래프를 바라보면 ,

매끄럽게 손실함수가 줄어드는 것을 알 수 있습니다.
이때까지 우리는 확률적 경사 하강법에서 배치 경사 하강법으로 바꾸어 모델을 설계했습니다.
앞에서 말했듯이 배치 경사 하강법은 모든 샘플에 대해 한번에 계산하는 방식입니다. 딥러닝에서는 종종 아주 많은 양의 데이터를 사용하는데 배치 경사 하강법은 이런경우 사용하기 어렵습니다. 그래서 실전에서는 확률적 경사하강법과 배치 경사 하강법의 절충안인 미니 배치 경사하강법을 씁니다.
-미니 배치 경사 하강법-
배치 경사하강법과 구현 방식이 비슷하지만 에포크마다 전체 데이터를 사용하는 것이 아니라 조금씩 나누어 정방향 계산을 수행하고 그레디언트를 구하여 가중치를 업데이트 합니다. 보통(16,32,64 ..)등 2의 배수를 사용합니다.
미니 배치 경사 하강법 구현
1)초기화 함수에 batch_size 매개 변수를 추가합니다.
def __init__(self, units=10, batch_size=32, learning_rate=0.1, l1=0, l2=0):
super().__init__(units, learning_rate, l1, l2)
self.batch_size = batch_size # 배치 크기
2)gen_batch() 메서드 만들기
제너레이터로 구현합니다. 제너레이터는 순차적으로 데이터에 접근할 수 있는 반복 가능한 객체(iterator)를 반환합니다. 제너레이터를 쓰면 명시적으로 리스트를 만들지 않으면서 필요한 데이터를 추출할 수 있습니다. (yield 사용)
def gen_batch(self, x, y):
length = len(x)
bins = length // self.batch_size # 미니배치 횟수
if length % self.batch_size:
bins += 1 # 나누어 떨어지지 않을 때
indexes = np.random.permutation(np.arange(len(x))) # 인덱스를 섞습니다.
x = x[indexes]
y = y[indexes]
for i in range(bins):
start = self.batch_size * i
end = self.batch_size * (i + 1)
yield x[start:end], y[start:end] # batch_size만큼 슬라이싱하여 반환합니다.gen_batch() 메서드는 전체 훈련 데이터 x,y를 전달받아 batch_size 만큼 미니 배치를 만들어 반환 한다. 그런다음 반환된 미니 배치 데이터 x_batch , y_batch를 training() 메서드에 전달한다.
3) fit() 메소드 에서 미니배치를 순회하는 for문을 추가합니다.
def fit(self, x, y, epochs=100, x_val=None, y_val=None):
y_val = y_val.reshape(-1, 1) # 타깃을 열 벡터로 바꿉니다.
self.init_weights(x.shape[1]) # 은닉층과 출력층의 가중치를 초기화합니다.
np.random.seed(42)
# epochs만큼 반복합니다.
for i in range(epochs):
loss = 0
# 제너레이터 함수에서 반환한 미니배치를 순환합니다.
for x_batch, y_batch in self.gen_batch(x, y):
y_batch = y_batch.reshape(-1, 1) # 타깃을 열 벡터로 바꿉니다.
m = len(x_batch) # 샘플 개수를 저장합니다.
a = self.training(x_batch, y_batch, m)
# 안전한 로그 계산을 위해 클리핑합니다.
a = np.clip(a, 1e-10, 1-1e-10)
# 로그 손실과 규제 손실을 더하여 리스트에 추가합니다.
loss += np.sum(-(y_batch*np.log(a) + (1-y_batch)*np.log(1-a)))
self.losses.append((loss + self.reg_loss()) / len(x))
# 검증 세트에 대한 손실을 계산합니다.
self.update_val_loss(x_val, y_val)
이렇게 해서 여러 경사하강법을 신경망에 구현해 봤습니다.
사이킷런에는 이미 신경망 알고리즘이 구현되었습니다. 간단히 살펴보겠습니다.
사이킷런 사용해 다층 신경망 훈련하기
1. MLPClassifer의 객체 만들기
from sklearn.neural_network import MLPClassifier
mlp = MLPClassifier(hidden_layer_sizes=(10, ), activation='logistic',
solver='sgd', alpha=0.01, batch_size=32,
learning_rate_init=0.1, max_iter=1000)
mlp.fit(x_train_scaled, y_train)
mlp.score(x_val_scaled, y_val)
hidden_layer_sizes : 은닉층의 크기를 정의.
> 은닉층의 수와 뉴런의 개수를 튜플로 전달합니다. 예를 들어 10개의 뉴런을 가진 2개의 은닉층을 만들려면 (10,10)과 같이 설정합니다. 이 매개변수의 기본값은(100,) 지금은 10개의 뉴런을 가진 하나의 은닉층 입니다.
activation : 활성화 함수를 지정.
> 시그모이드함수를 이용하기위해 logistic 으로 지정하였습니다. 이 매개변수의 기본값은 ReLU입니다.
solver : 경사 하강법 알고리즘 지정.
> 기본값은 확률적 경사 하강법 (sgd)
alpha : 규제를 적용하기 위한 매개변수
> 일반적으로 L1규제는 효과가 크지 않기 때문에 사이킷런 신경망모델은 L2 규제만 지원합니다.

포스팅이 좋았다면 "좋아요❤️" 또는 "구독👍🏻" 해주세요!



